Introduction:

K-Means is one of the most important algorithms when it comes to machine learning training In this blog, we will understand the K-Means clustering algorithm with the help of examples.

A Hospital Care chain wants to open a series of Emergency-Care wards within a region. We assume that the hospital knows the location of all the maximum accident-prone areas in the region. They have to decide the number of the Emergency Units to be opened and the location of these Emergency Units, so that all the accident-prone areas are covered in the vicinity of these Emergency Units.

The challenge is to decide the location of these Emergency Units so that the whole region is covered. Here is when K-means Clustering comes to rescue!

Before getting to K-means Clustering, let us first understand what Clustering is.

A cluster refers to a small group of objects. Clustering is grouping those objects into clusters. In order to learn clustering, it is important to understand the scenarios that lead to cluster different objects. Let us identify a few of them.

Clustering : 

Clustering is dividing data points into homogeneous classes or clusters:

• Points in the same group are as similar as possible
• Points in different group are as dissimilar as possible

When a collection of objects is given, we put objects into group based on similarity.

Application of Clustering:

Clustering is used in almost all the fields. You can infer some ideas from Example 1 to come up with lot of clustering applications that you would have come across.

Listed here are few more applications, which would add to what you have learnt.

• Clustering helps marketers improve their customer base and work on the target areas. It helps group people (according to different criteria’s such as willingness, purchasing power etc.) based on their similarity in many ways related to the product under consideration.
• Clustering helps in identification of groups of houses on the basis of their value, type and geographical locations.
• Clustering is used to study earth-quake. Based on the areas hit by an earthquake in a region, clustering can help analyse the next probable location where earthquake can occur.

Clustering Algorithms:

A Clustering Algorithm tries to analyse natural groups of data on the basis of some similarity. It locates the centroid of the group of data points. To carry out effective clustering, the algorithm evaluates the distance between each point from the centroid of the cluster.

The goal of clustering is to determine the intrinsic grouping in a set of unlabelled data.

i

 K-means Clustering : 

K-means (Macqueen, 1967) is one of the simplest unsupervised learning algorithms that solve the well-known clustering problem. K-means clustering is a method of vector quantization, originally from signal processing, that is popular for cluster analysis in data mining.

Example:

A pizza chain wants to open its delivery centres across a city. What do you think would be the possible challenges?

• They need to analyse the areas from where the pizza is being ordered frequently.
• They need to understand as to how many pizza stores has to be opened to cover delivery in the area.
• They need to figure out the locations for the pizza stores within all these areas in order to keep the distance between the store and delivery points minimum.

Resolving these challenges includes a lot of analysis and mathematics. We would now learn about how clustering can provide a meaningful and easy method of sorting out such real life challenges. Before that let’s see what clustering is.

K-means Clustering Method:

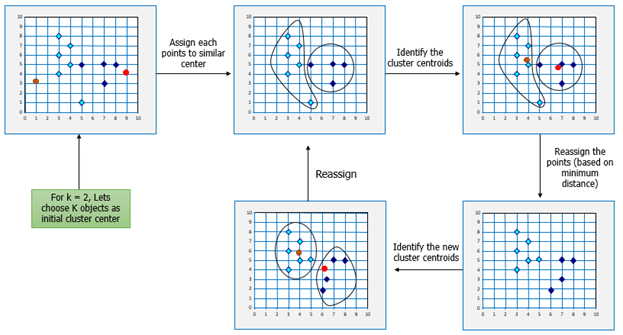
If k is given, the K-means algorithm can be executed in the following steps:

• Partition of objects into k non-empty subsets
• Identifying the cluster centroids (mean point) of the current partition.
• Assigning each point to a specific cluster
• Compute the distances from each point and allot points to the cluster where the distance from the centroid is minimum.
• After re-allotting the points, find the centroid of the new cluster formed.

Mathematical Formulation for K-means Algorithm:

D= {x1,x2,…,xi,…,xm} à data set of m records

xi= (xi1,xi2,…,xin) à each record is an n-dimensional vector

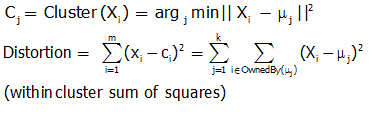
Finding Cluster Centers that Minimize Distortion:

Solution can be found by setting the partial derivative of Distortion w.r.t. each cluster center to zero.

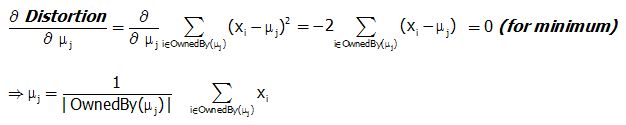
For any k clusters, the value of k should be such that even if we increase the value of k from after several levels of clustering the distortion remains constant. The achieved point is called the “Elbow”.

This is the ideal value of k, for the clusters created.